 |
 |
- Search
| Asian Spine J > Volume 12(5); 2018 > Article |
|
Abstract
Overview of Literature
Certain occupational environments in civilian and military populations may affect the cervical spine of individuals by cyclic loading. Research on this mechanism is scarce.
Methods
Here, we developed a finite element model of the human C4–C5 disc. It comprised endplates, five layers of fibers, a nucleus, and an annulus ground substance. The endplates, ground substance, and annular fibers were modeled with elastic, hyperviscoelastic, and hyper-elastic materials, respectively. We subjected the disc to compressive loading (150 N) for 10,000 cycles at frequencies of 2 Hz (low) and 4 Hz (high). We measured disc displacements over the entire loading period. We obtained maximum and minimum principal stress and strain and von Mises stress distributions at both frequencies for all components. Further, we used contours to infer potential mechanisms of internal load transfer within the disc components.
Results
The points of the model disc displacement versus the loading cycles were within the experimental corridors for both frequencies. The principal stresses were higher in the ground matrix, maximum stress was higher in the anterior and posterior annular regions, and minimum stress was higher along the superior and inferior peripheries. The maximum principal strains were radially directed, whereas the minimum principal strains were axially/obliquely directed. The stresses in the fibers were greater and concentrated in the posterolateral regions in the innermost layer.
Conclusions
Disc displacement was lower at high frequency, thus exhibiting strain rate stiffening and explaining stress accumulation at superior and interior peripheries. Greater stresses and strains at the boundaries explain disc injuries, such as delamination. The greater development of stresses in the innermost annular fiber layer (migrating toward the posterolateral regions) explains disc prolapse.
Biomechanical studies of the human spine help determine external and internal responses to day-to-day activities, such as those occurring in occupational environments [1]. Clinical, experimental, and computational models are used to investigate the behavior of the spine. Clinical models are used to obtain in vivo data, whereas experimental models using human cadavers are used to determine external responses of the spine, such as the range of motion. A majority of experimental studies have focused on physiological models, particularly under pure moment-based, quasi-static or static, flexion, extension, lateral bending, and axial rotation loads [1]. Such modalities continue to drive developments for newer applications, such as cervical and lumbar spine artificial discs, in the field of spine biomechanics. In physiological models, the load application to the spine predominantly belongs to the single-cycle type.
Other studies have focused on traumatic models by delivering loads to the spine via contact or non-contact forces; contact loading to the head is applied to simulate automotive and sporting events. These studies have determined fracture loads and described human neck injury tolerances [2]. Inertial or non-contact loading is applicable to automotive rear impacts. Research in this area is mainly aimed at understanding whiplash-associated disorders. Tests using human cadaver models have delineated the role of demographic factors based on differences in intervertebral space and segmental kinematics [3]. The insult is applied to the spine in one cycle in these traumatic loading events.
From an occupational perspective, certain civilian and military occupations subject the human spine to repeated loading. Exposure to whole body vibrations from industrial workplace duties have long been recognized as a mechanical cause, further predisposing to long-term complications, such as lower-back pain, stemming from radicular symptoms, and disc-related issues involving annular fibers and endplates. Over the past five decades, studies have been conducted using cadaver lumbar spinal columns and segments to understand the cyclic loading response [4]. Injuries in cadavers can be used to search for correlations with in vivo lesions caused by repeated loading activities in civilian populations.
From a military perspective, certain operational activities, such as specific personnel training, can induce cyclic loading on the neck [5]. The prevalence of neck pain in helicopter pilots exposed to repeated load ranges from 29% to 57% [5-8]. The helmet worn adds its mass to the natural in vivo head weight. Devices, such as night vision goggles, visor, and communications combo, also add to the physical properties of the helmet and head. The increased mass, moment of inertia, and center of gravity shift due to helmet- and head-mounted devices place additional loads on the cervical spine during normal military training and operational activities. Because such activity-based loads in the military are cyclic and because vertebral fractures are uncommon, the most susceptible regions for potential injury or weakening of the spine are the disc and/or the endplates. The axial load on the cervical spine column caused by the head-supported mass has not been completely investigated under cyclic loading conditions. An investigation regarding internal responses, such as stresses and strains and their distributions, is needed to better understand the biomechanics of helmet-wearing situations. Therefore, here, we aimed to use a simplified finite element (FE) model of the human cervical disc and apply axial cyclic loading similar to the head-supported mass sustained by military personnel wearing helmets. We used internal response outputs to offer explanations for clinical disc disorders of the human cervical spine.
We developed the FE model of the human C4–C5 disc using computed tomography images imported into commercial software. We performed vertebral segmentation using bone threshold frequency. We exported the segmented images in a stereo-lithographic format for further processing in the Altair Hypermesh software. We selected the vertices surrounding the endplate locations based on the adjacent vertebral bodies. The chosen vertices on the vertebral bodies defined the bony endplate boundaries of the disc. The cartilaginous and bony endplates were meshed with quadratic elements, and we developed a hexahedral mesh of the disc annulus and nucleus using the superior and inferior endplates as references (Fig. 1).
We modeled the nucleus pulposus and annulus ground substance using solid hexahedral elements; the annular fibers were modeled with five pairs of concentric quadratic shell layers embedded in the ground substance. The rationale for using the five pairs of layers is described later. We modeled the superior and inferior cartilaginous and bony endplates using shell elements. The element size for the model was 0.5 mm, and the model contained 8,740 solid hexahedral and 18,636 quadratic shell elements.
We obtained the material properties for the ground substance from experimental data [4]. Properties of the endplates, nucleus, and annular fiber components of the disc were obtained from literature studies (Table 1). The annular ground substance was modeled as a hyperviscoelastic material. We obtained the elastic properties for the annulus from tension–compression experiments and the viscous properties from stress–relaxation tests. We exported the curves from the experiments into the Abaqus software. The stress–strain data from the tension–compression experiments and stress–relaxation data were directly used as inputs into the Abaqus software for the Aruda–Boyce hyper-elastic material. The nucleus was modeled using an incompressible elastic material with a modulus of 1 MPa and a Poisson’s ratio of 0.45 [9,10]. The annular fibers were modeled as hyper-elastic materials, and tension-only material properties varied from the innermost to the outermost layer. We used a value of 0.4 for the Poisson’s ratio for the ground substance [11,12]. We included the gradual change in the fiber angle with the radial position in the model: fiber angles ±25° in the outer layers to ±45° in the inner layers; the elastic modulus and Poisson’s ratio of the bony endplates were 5,600 MPa and 0.3, respectively [13]. These values for the cartilaginous endplates were 24 MPa and 0.4, respectively.
The inferior bony endplate was constrained at all degrees-of-freedom. We applied a uniform load of 150 N at 2 and 4 Hz (low and high frequency) to the superior endplate for 10,000 cycles. The model results were outputted as displacements of the superior endplate over the entire cyclic loading, and we compared them with the corresponding experimental data for validation purposes [4]. We obtained residual stresses and strains in the annulus, nucleus, and annular fibers at the end of cyclic loading. We used the stress–strain profiles to infer the potential mechanisms of load transfer and disc injury from cyclic loading.
We compared the displacement of the superior endplate during the entire cyclic loading period with the experimental data at both low and high frequencies (Fig. 2). The model-predicted displacements were within the mean±1 standard deviation corridors of the test data. The displacement was greater during the initiation of the loading process and reduced exponentially in the first 2,000 cycles for the lower frequency and 1,000 cycles for the higher frequency. The displacement magnitudes were lower at the high frequency.
At the low frequency, the maximum (tensile) and minimum (compressive) principal stresses were higher in the annulus ground matrix than in the nucleus and annular fibers (Fig. 3). The maximum stress was higher in the anterior and posterior annular regions (regions toward the red color, Fig. 3). Further, the minimum stress was higher along the superior (blue color, Fig. 3) and inferior periphery of the disc. The pattern was similar at the high frequency, with lower amplitudes (Fig. 4). The compressive stresses were higher than the tensile stresses at both frequencies.
At both frequencies, the maximum principal strains were radially directed, whereas the minimum principal strains (Figs. 5, 6) were axially and/or obliquely directed. The tensile and compressive strain vector amplitudes were higher at the low loading frequency (Fig. 5) than at the high loading frequency (Fig. 6).
At the low frequency, the von Mises stress distributions were transmitted across the cross-section of the annulus (Fig. 7); however, at the high frequency, they were concentrated at the superior and inferior boundaries (Fig. 8). At both frequencies, the stresses in the annular fibers were greater in the posterior regions in the innermost layer and were concentrated near the posterolateral region of the disc (Figs. 7, 8). At both frequencies, the stress distributions in the nucleus were greater in the anterior and posterior directions; however, the stress was distributed in a larger area at the low frequency.
Cyclic loading of the neck occurs in civilian and military occupational environments; however, individuals in military environments are subject to specific variables that render them more prone to suffering neck injuries from cyclic loading (e.g., head-supported masses, i.e., wearing of military helmets and their devices for longer periods) [14,15]. While the etiology of neck pain is multifactorial, biomechanical loading has been identified as a major external stress factor causing long-term changes, including cervical spondylosis. The identified pathways in civilian cases begin with biomechanical loads resulting in internal and physiological responses, causing mechanical strain and fatigue, thus leading to pain, discomfort, and impairment; loading repetitiveness is an important risk factor. Operating or driving of vibrating equipment has been positively associated with prolapsed discs in civilian environments. Changes in muscular activities caused by prolonged use of head-supported masses alter the muscular activity, as in low-velocity impacts, and result in pain [16]. In patients with known mechanisms of injury, 14% used Kevlar helmets, and noncombat operations accounted for 96% of all neck pains in a military-specific study [14]. Longer wearing periods of such helmets that are heavier than those used by civilians and carrying heavy backpacks were attributed as reasons for the predisposition of military personnel to neck pain. The number of hours and repeated exposure accelerations and the use of head-mounted devices, such as night vision goggles, helmets, and oxygen masks, were identified in the etiology of flight-related neck pain in military pilots and airmen [17-21]. Extreme vibration was also considered a risk factor [8]. Although brief, these studies indicate that cyclic loading of the human head-neck occurs in both civilian occupational and military fields, with the head-supported mass acting as an added contributing factor in the military environments.
We aimed to explain clinical observations of disc disorders based on internal responses using a disc FE model. The loading magnitude represented the axial compressive forces sustained by the disc in military situations with head-supported masses, i.e., the helmet used in training and operational activities [22]. The model responses, expressed as disc displacement over the entire loading period, were within the experimental corridors. This validation process has been accepted in spine biomechanics studies with quasi-static and dynamic loadings [23-25].
Lower displacements at the high frequency indicate a strain rate-stiffening phenomenon (Fig. 2) associated with the disc responding to increasing loading rates with increased stiffness. This phenomenon has also been reported for lumbar discs. From this perspective, cyclic responses of the two regions of the spine are similar. While the experiments and present modeling results show a plateau of the response after 1,000–2,000 cycles of loading, the stress analysis outputs revealed additional insights into the internal mechanics of the disc components and assisted us in drawing clinical correlations.
The viscoelastic behavior of the annulus (simulated as a hyperviscoelastic material) contributed to the exponential reduction of disc displacement. A viscoelastic material is represented with a spring and a dashpot system, with the former representing elasticity and the latter representing the viscous behaviors. After applying the external force, the elastic and viscous components shared the strain in the annulus. With the removal of the force during the unloading phase, the strain in the elastic part instantaneously recovered, whereas the strain in the viscous component took time to recover. However, the next compression loading cycle started before the full recovery of the strain. The residual strain from the previous cycle caused the force to reach 150 N with lesser displacement. This phenomenon resulted in the exponential reduction in response over the number of cycles.
The greater magnitude of the minimum principal stress and its concentration around the annulus periphery indicates an internal mechanism of load transfer. The lower magnitudes of the compressive stresses at the high frequency indicate that the cervical disc does not get time to react to the applied axial loading. This process may result in the accumulation of stress concentration in the superior and inferior boundaries of the disc, thus leading to local failures at the interface between the annulus and the endplates at the high frequency. The radial development of tensile strain and axial/oblique development of compressive strain shows that disc response is multimodal, although the loading is uniaxial. Therefore, we used von Mises stresses to understand the multimodal effects.
The distribution of the von Mises stresses over the thickness of the disc at the low frequency and their localization near the boundaries at the high frequency indicate the following: with increasing loading rates, the time required to transmit the stresses along the cross-section is reduced, thereby resulting in stress accumulation at the boundaries. This pattern may be clinically relevant. Asymmetric distributions in the stress patterns between the two frequencies, along with differences in the stress concentration patterns (higher at the boundaries and lesser stress concentration area with increases in frequency) indicate the likelihood of disc injury at the high frequency. The stress concentration at the posterior boundaries may lead to delamination of the annulus and endplates emanating from the posterior region (Figs. 7, 8). The development of gradients due to localized stresses is a risk factor for the delamination in lumbar spine aging-related disc and degeneration studies. Clinical studies in the area (not cited due to limitations in the number of references) have also implicated vibration/cyclic loading in accelerated disc degeneration leading to delamination. Studies concerning the cervical spine with repeated loading simulating military environments are few; however, based on the prevalence of neck pain in this population and the similarities between the lumbar and cervical disc components, it is reasonable to infer that the cervical discs are also susceptible to delamination. In addition, the cervical intervertebral discs also degenerate with increasing age (similar to lumbar discs), further supporting this idea.
The greater nucleus stresses in the anterior and posterior directions indicate that under axial loading, the incompressible nucleus attempts to move preferentially along these directions. This movement is constrained by the innermost fiber layer, thus resulting in greater stresses in the posterolateral region. The stress concentration in the posterolateral regions of annular fibers may explain disc prolapse. In addition, these observations suggest that the mechanism of disc prolapse originates from the greatest stresses sustained by the innermost annular fibers transmitted to the outer layers. Cervical prolapse and disc herniation has been reported in civilian and military studies (not cited due to constraints in the number of references). From these perspectives, our study has provided additional insights into the internal mechanics of the disc and has offered an explanation for disc delamination and the propensity to initiate prolapse in the posterolateral regions, which are clinically relevant in both civilian and military populations.
Cervical disc herniation has been classified into central, para-central, posterolateral and lateral types [26-28]. One study reported a review of 745 cases of disc lesions, out of which lateral disc accounted for 607 (82%, soft type) and 95 (13%, hard type) of the cases, central spondylosis for 32 (4.3%), and central soft disc herniation for eight (1.0%) [29]. In a follow-up study involving surgical patients, data were reported from 296 cases: 246 (83%) from lateral soft and hard discs, 39 (13.2%) from spondylosis, and 11 (3.7%) from central/para-central soft discs [27]. Of those 11, there were seven cases of central and four cases of para-central herniation [27]. Other studies have reported greater numbers of para-central than posterolateral cases: from eight cases, five were para-central and three were posterolateral [30], and from 34 cases, 22 were paracentral and 12 were posterolateral [28]. While the results from our study explain the posterolateral mechanism, other loading modes, such as flexion–extension may have to be considered to explain the para-central mechanism.
The present study used compressive loading; however, in vivo, the human cervical spine sustains complex loading including flexion and extension. We used compression for our cyclic loading experiments. However, to include other modes, it would be necessary to first conduct cyclic loading tests under those modes, use test data to validate the FE model, and then use its outputs, such as stresses, to delineate the injury mechanisms. In principle, this may be achieved using the same process used in the present investigation; however, we focused on the compression mode in our FE model. Another limitation is that our model applies only to the cervical spine and excludes the lumbar spine where disc injuries are common. We limited our study to two frequencies, because of the availability of experimental data. Additional studies are warranted to relax these limitations and achieve wider applications for other spinal regions, loading modes, and frequencies.
We developed a FE model of the human C4–C5 disc; it comprised five layers of annulus fibers, a nucleus pulposus, ground substance, and endplates with appropriate material and element definitions. We validated the model using experimental data from C4–C5 disc segments under a compressive loading of 150 N for 10,000 cycles at two frequencies. Disc displacement was lower at high frequency, thus exhibiting strain rate stiffening and explaining stress accumulation at superior and interior peripheries. Greater stresses and strains at the boundaries may explain disc injuries, such as delamination. The greater development of stresses in the innermost annular fiber layer migrating toward the posterolateral regions may explain disc prolapse.
Acknowledgments
This material is the result of work supported with resources and use of facilities at the Zablocki Veterans Administration Medical Center (ZVAMC), Milwaukee, Wisconsin, the Department of Neurosurgery at the Medical College of Wisconsin (MCW), and the U.S. Army Medical Research and Materiel Command, Fort Detrick, Maryland, W81XWH-16-1-0010. The MCW authors are part time employees of the ZVAMC. Any views expressed in this article are those of the authors and not necessarily representative of the funding organizations.
Fig. 1.
The model showing the disc with annulus, nucleus, and annular fibers embedded in the annular ground matrix.

Fig. 2.
Comparison of the model-predicted cyclic loading response (curve) with experimental corridors (shaded) at low (A) and high (B) frequency loadings. FEM, finite element method.

Fig. 3.
Maximum (A) and minimum (B) principal stress distributions in the disc at the low frequency loading. Avg, average.
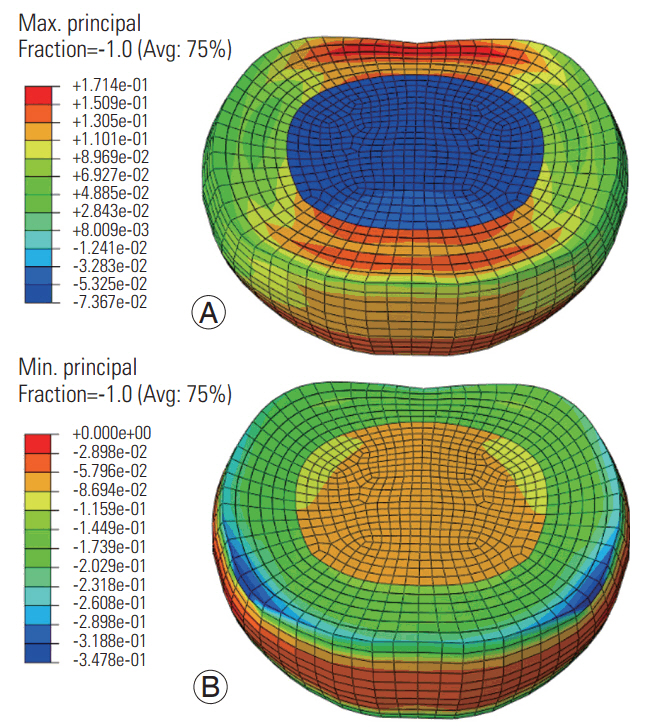
Fig. 4.
Maximum (A) and minimum (B) principal stress distributions in the disc at the high frequency loading. Avg, average.
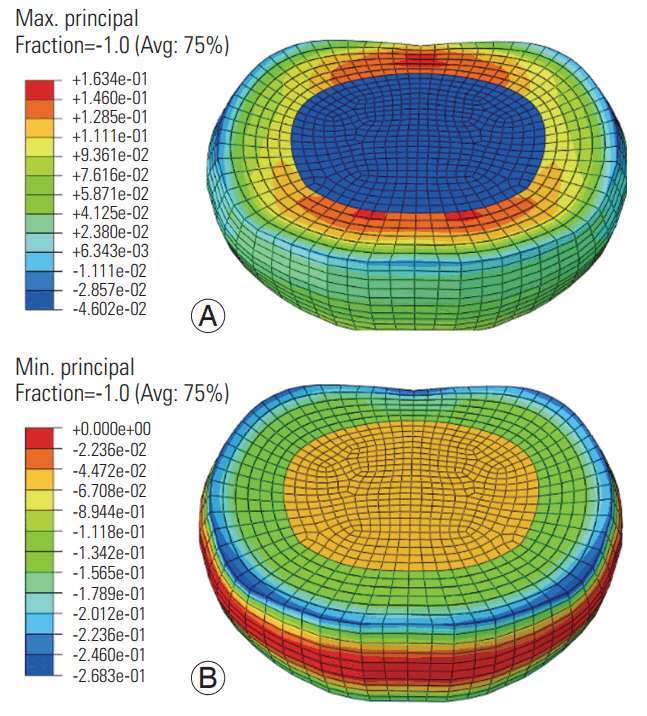
Fig. 5.
Maximum (A) and minimum (B) principal strain distributions in the disc simulated at the low frequency loading.
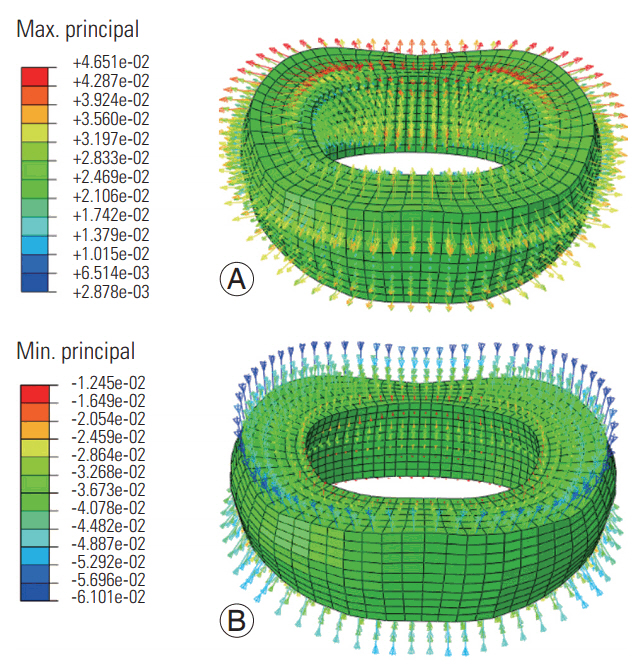
Fig. 6.
Maximum (A) and minimum (B) principal strain distributions in the disc simulated at the high frequency loading.

Fig. 7.
Von Mises stress distribution in the annulus (A), nucleus (B), and annular fibers (C) at the low frequency loading. Red regions indicate largest magnitudes. Blue shows the smallest magnitudes. Arrows show the posterolateral regions with the largest stresses. Avg, average.

Fig. 8.
Von Mises stress distribution in the annulus (A), nucleus (B), and annular fibers (C) at the high frequency loading. Red regions indicate largest magnitudes. Blue shows the smallest magnitudes. Arrows show the posterolateral regions with the largest stresses. Avg, average.
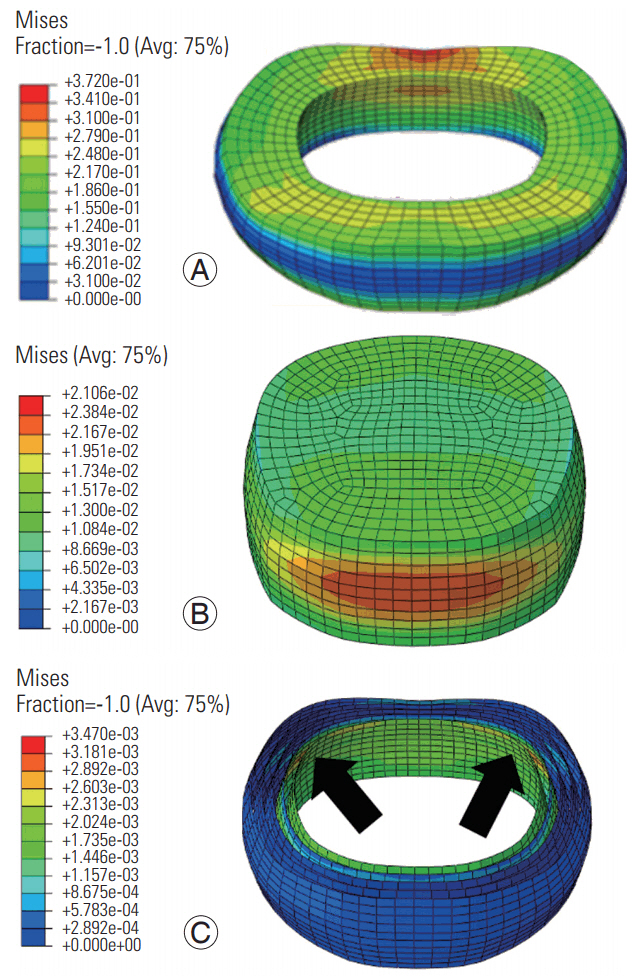
Table 1.
Material properties of the disc components
| Component | Material | Material properties | References |
|---|---|---|---|
| Bony endplates | Elastic | E=5,600 MPa, p=0.3 | |
| Cartilaginous endplates | Elastic | E=24 MPa, Mu=0.4 | |
| Nucleus | Elastic | E=1 MPa, p=0.45 | [16] |
| Annulus ground matrix | Arruda-Boyce hyper-viscoelastic | µ0=0.35 MPa, λm=7.00, D=1.2, G0=0.45, G∞=0.38, β=12.8 | [8] |
| Annular fibers (innermost) | Arruda-Boyce hyper-elastic | µ0=4.5*10-02 MPa, λm=7.00, D=14.8 | |
| Annular fibers (second from inner) | µ0=3.85*10-02 MPa, λm=7.00, D=17.3 | ||
| Annular fibers (third from inner) | µ0=7.49*10-03 MPa, λm=7.00, D=87.9 | ||
| Annular fibers (forth from inner) | µ0=7.68*10-03 MPa, λm=7.00, D=85.65 | ||
| Annular fibers (outermost) | µ0=7.95*10-03 MPa, λm=7.00, D=82.87 |
References
1. Cervical Spine Research Society Editorial Committee; Clark CR, Benzel EC, et al. The cervical spine. 4th ed. Philadelphia (PA): Lippincott Williams & Wilkins; 2005.
2. Nightingale RW, Myers BS, Yoganandan N,Neck injury biomechanics. Yoganandan N, Nahum AM, Melvin JW, editors. Accidental injury: biomechanics and prevention. 3rd ed. New York (NY): Springer; 2015. p.259–308.
3. Stemper BD, Yoganandan N, Pintar FA. Gender dependent cervical spine segmental kinematics during whiplash. J Biomech 2003 36:1281–9.


4. Yoganandan N, Umale S, Stemper B, Snyder B. Fatigue responses of the human cervical spine intervertebral discs. J Mech Behav Biomed Mater 2017 69:30–8.


5. Ang B, Harms-Ringdahl K. Neck pain and related disability in helicopter pilots: a survey of prevalence and risk factors. Aviat Space Environ Med 2006 77:713–9.

6. Balasubramanian V, Dutt A, Rai S. Analysis of muscle fatigue in helicopter pilots. Appl Ergon 2011 42:913–8.


7. Bridger RS, Groom MR, Jones H, Pethybridge RJ, Pullinger N. Task and postural factors are related to back pain in helicopter pilots. Aviat Space Environ Med 2002 73:805–11.

8. Cohen SP, Gallagher RM, Davis SA, Griffith SR, Carragee EJ. Spine-area pain in military personnel: a review of epidemiology, etiology, diagnosis, and treatment. Spine J 2012 12:833–42.


9. Jones JA, Hart SF, Baskin DS, et al. Human and behavioral factors contributing to spine-based neurological cockpit injuries in pilots of high-performance aircraft: recommendations for management and prevention. Mil Med 2000 165:6–12.


10. Qasim M, Natarajan RN, An HS, Andersson GB. Damage accumulation location under cyclic loading in the lumbar disc shifts from inner annulus lamellae to peripheral annulus with increasing disc degeneration. J Biomech 2014 47:24–31.


11. Ng HW, Teo EC. Nonlinear finite-element analysis of the lower cervical spine (C4-C6) under axial loading. J Spinal Disord 2001 14:201–10.


12. Yoganandan N, Kumaresan S, Voo L, Pintar FA. Finite element applications in human cervical spine modeling. Spine (Phila Pa 1976) 1996 21:1824–34.


13. Pitzen T, Schmitz B, Georg T, et al. Variation of endplate thickness in the cervical spine. Eur Spine J 2004 13:235–40.



14. Cohen SP, Kapoor SG, Nguyen C, et al. Neck pain during combat operations: an epidemiological study analyzing clinical and prognostic factors. Spine (Phila Pa 1976) 2010 35:758–63.


15. Bongers PM, Ijmker S, van den Heuvel S, Blatter BM. Epidemiology of work related neck and upper limb problems: psychosocial and personal risk factors (part I) and effective interventions from a bio behavioural perspective (part II). J Occup Rehabil 2006 16:279–302.


16. Kumar S, Narayan Y, Prasad N, Shuaib A, Siddiqi ZA. Cervical electromyogram profile differences between patients of neck pain and control. Spine (Phila Pa 1976) 2007 32:E246–53.


17. Andersen HT. Neck injury sustained during exposure to high-G forces in the F16B. Aviat Space Environ Med 1988 59:356–8.

18. Green ND. Acute soft tissue neck injury from unexpected acceleration. Aviat Space Environ Med 2003 74:1085–90.

19. Hamalainen O, Vanharanta H, Bloigu R. Determinants of +Gz-related neck pain: a preliminary survey. Aviat Space Environ Med 1993 64:651–2.

20. De Loose V, van den Oord M, Burnotte F, et al. Individual, work-, and flight-related issues in F-16 pilots reporting neck pain. Aviat Space Environ Med 2008 79:779–83.


21. Van den Oord MH, de Loose V, Meeuwsen T, Sluiter JK, Frings-Dresen MH. Neck pain in military helicopter pilots: prevalence and associated factors. Mil Med 2010 175:55–60.


22. Motiwale S, Subramani AV, Zhou Z, et al. Damage prediction for a cervical spine intervertebral disc. In: Proceedings of the International Mechanical Engineering Congress & Exposition; 2016 Nov 13-17; Phoenix, USA.

23. Kumaresan S, Yoganandan N, Pintar FA, Maiman DJ. Finite element modeling of the cervical spine: role of intervertebral disc under axial and eccentric loads. Med Eng Phys 1999 21:689–700.


24. Kumaresan S, Yoganandan N, Pintar FA, Maiman DJ, Goel VK. Contribution of disc degeneration to osteophyte formation in the cervical spine: a biomechanical investigation. J Orthop Res 2001 19:977–84.


25. Yoganandan N, Kumaresan S, Voo L, Pintar FA. Finite element model of the human lower cervical spine: parametric analysis of the C4-C6 unit. J Biomech Eng 1997 119:87–92.


26. Aronson N, Filtzer DL, Bagan M. Anterior cervical fusion by the smith-robinson approach. J Neurosurg 1968 29:396–404.


27. Scoville WB, Dohrmann GJ, Corkill G. Late results of cervical disc surgery. J Neurosurg 1976 45:203–10.


- TOOLS
-
METRICS

- Related articles in ASJ
-
Biomechanics of Degenerative Spinal Disorders2016 April;10(2)





